「理数系離れが進んだ原因の一つは、子どもたちに、頭だけで考えさせているからだと思います。元来、勉強の原動力は好奇心。今の子どもたちは、数学の公式や定理を習っても、テストや受験のために覚えるだけだから、それが終われば忘れてしまう。でも、子どもたちをワクワクさせて好奇心を刺激し、作業を通して『なるほど、そうだったのか!』と納得できる経験をさせれば、頭に残るし、学ぶことの楽しさを体で知ることにもなる。そうすれば、今度は自分で面白いと思うものを見つけて、自発的に学びを深めていくようになりますよ。だから、まずは興味を持たせることが大切です」(数学者•秋山仁)
昨日は、町営塾の生徒へ《代数》→支援学校の生徒へ《幾何学》と数学のダブルヘッダー授業。
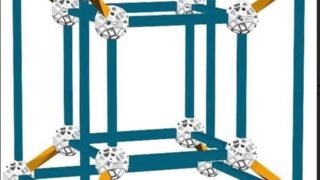
プラトン立体をテーマにした連続ワークショップ第6弾!
今回のテーマは「面と辺と頂点の関係」
手で磁石をつかって、付けたり、外したりを繰り返しながら、立体作成に取り組む姿は、まるで操り人形にも見えてくる。
プラトン立体を自由自在に操るパペッティアへの道!?
《辺の数》
まずは、面が一番少ない正四面体で検証。
①正四面体の各面は正三角形なので、辺の数はのべ 4×3=12本であることを確認。
②しかし、1つの辺は 2つの面に接しているので、二重に数えられることを確認。
③なので正四面体の辺の数は、4×3÷2で6本
正六面体は、6×4÷2で12本
正八面体は、8×3÷2で12本
正十二面体は、12×5÷2で30本
正二十面体は、20×3÷2で30本
④つまり、正四面体の辺の数の出し方は、
(辺の数)=(面の辺の数)×(面の数)÷2
《頂点の数》
これも、まずは、面が一番少ない正四面体で検証。
①正四面体の各面は正三角形なので、頂点の数はのべ 4×3=12本であることを確認
②しかし、1つの頂点は 3つの面が集まっているので、三重に数えられていることを確認
③なので、よって、正四面体の頂点の数は、4×3÷3=4個
正六面体は、6×4÷3で8個
正八面体は、8×3÷4で6個
正十二面体は、12×5÷3で20個
正二十面体は、20×3÷5で12個
④つまり、正多面体の頂点の数の出し方は、
(頂点の数)=(面の頂点の数)×(面の数)÷(1点に集まる面の数)
最後に、正十二面体に立方体が内接するワーク。ケプラーの世界につながる正多面体の関係性への第一歩!
ミクロからマクロまで統合する世界観へ!
#プラトン立体 #ケプラー #辺と面と頂点 #オイラー #理系離れ #秋山仁